127
ЗАМЕЧАНИЯ К ТЕОРИИ ТОЧНОСТИ БЫСТРЫХ ДВИЖЕНИЙ, ПРЕДЛОЖЕННОЙ Р. ШМИДТОМ С СОАВТОРАМИ
И. Е. ЦИБУЛЕВСКИЙ
Впервые в истории исследований психофизиологических механизмов, управляющих произвольными движениями, разработана математически формализованная модель управления [3]. Модель представляет собой дальнейшее развитие идеи Р. Шмидта [2] об управлении движением по разомкнутой схеме, т. е. без корректирующего, воздействия обратных связей, на основании «схемы» или моторной программы. Хранящаяся в памяти программа является единой для всех движений данного вида. В каждом отдельном случае, в соответствии с заданными величинами протяженности и времени движения, для программы подбираются определенные значения ее
128
параметров. В таком виде программа задает, какие именно мышцы, с какими усилиями и в какой временной последовательности должны сократиться. Так, например, если рука переносится за время T на расстояние S, то путь s (t), скорость v (t) и усилие F (t) изменяются как некоторые функции времени (см. рис.). Очевидно, общий путь S отвечает площади под кривой v (t). Максимальная скорость руки обозначена через Vm. Площади под положительной частью кривой изменения силы F(t) изображает положительный импульс I этой силы, продолжительность которого обозначена через Ti. Отрицательный импульс (—I) останавливает руку в момент Т. Максимальная величина положительной силы обозначена как Fm. Программой движения в данном случае авторы считают форму кривой F(t), а параметрами программы — максимальную силу Fm и время импульса Ti. Это равносильно допущению, что при изменении заданных величин S и T кривая F(t) равномерно вытягивается (или сокращается) как по горизонтали, так и по вертикали, т. е. изменяется ее масштаб вдоль координатных осей, но сохраняется форма.
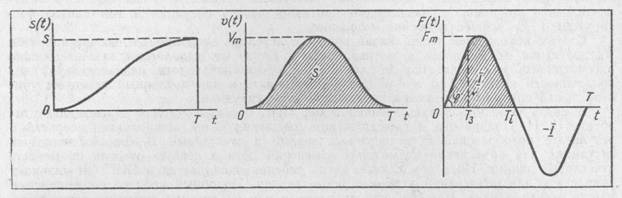
Каждому заданию S и T соответствует одна определенная пара значений параметров Fm и Ti. Ошибка в положении руки в момент окончания движения вызывается тем, что фактически реализованные в движении величины параметров отличаются от требуемых или, другими словами, рассеивание случайной величины S связано с рассеиванием также случайных величин параметров Fm и Ti.
Такую модель явления авторы применили для
анализа точности выполнения человеком быстрых движений трех видов: 1)
одноприцельные движения с заданными величинами перемещения A и времени T; 2) одиночные
неприцельные движения с заданными A и T; 3) возвратно-поступательные движения с заданным ритмом.
Относительно случайных величин Fm и Ti принято допущение, что они независимы и их средние
квадратические отклонения σ[Fm] и σ[Ti] пропорциональны математическим ожиданиям ![]() и
и ![]()
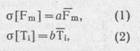
где а и b — коэффициенты пропорциональности.
Анализ выполнен почти без помощи математического аппарата путем логических построений и по этой причине привел не к количественным, а к качественным выводам, в виде характера зависимости рассеивания ошибки движения от перемещения A и времени T. На основании анализа авторы пришли к общему заключению, что модель правильно объясняет механизм управления если не всеми, то многими видами движений и применима не только к быстрым, но и к медленным движениям.
Теоретический анализ и выводы авторов нуждаются в критических замечаниях:
1) Под одноприцельным движением в работе понимается следующее. Рука, удерживающая до начала движения острие небольшой указки в стартовой точке на поверхности стола, переносится справа налево с задачей возможно точнее попасть острием в линию-цель. Движение должно быть выполнено за заданный интервал времени, который усваивается испытуемым при тренировочных пробах.
Применяя рассмотренную модель для анализа
точности движения этого вида, авторы в ходе рассуждений допустили ошибку,
существенно исказившую результат и приведшую к неверному выводу, что диапазон
полного разброса точек попадания We пропорционален
отношению ![]()
Приводим в сжатом виде верное решение задачи. На основании принятого в модели допущения о неизменности формы кривой F(t) можно написать следующие уравнения:
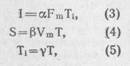
129
где α, β, γ – коэффициенты, однозначно определяемые видом кривой F (t). Дополнив эти уравнения уравнением количества движения:
![]()
в котором M – масса указки с учетом приведенной к ней массы руки, получаем систему, полностью определяющую зависимость пути S от параметров программы Fm и Ti. Действительно, исключив из уравнений (3)-(6) величины I, T и Vm, находим:
![]()
Для определения математического ожидания и среднего квадратического отклонения случайной величины S найдем предварительно эти характеристики для Ti2.
Проще всего получить из приближенные значения, воспользовавшись методом линеаризации функции случайного аргумента [1]. Если σ[Ti] малая величина, то:
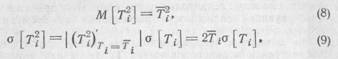
или после подстановки (2) в (9):
![]()
На основании известной формулы для математического ожидания произведения двух случайных величин X и Y [1]:
![]()
где Kxy – корреляционный момент связи X и Y, имея в виду, что Fm и Ti независимы, а значит, независимыми и Fm и Ti2 , находим:
![]()
Дисперсия произведения двух независимых случайных величин определяется формулой:
![]()
По этой формуле с учетом (1), (8) и (9) находим:
![]()
где c2=4a2b2+4b2+a2,
и соответственно:
![]()
На основании (7) и (15):
![]()
При помощи (7) и (12) получаем математическое ожидание M[S]:
![]()
Полагая, что центр рассеивания точек попадания находится на линии-цели, т. е.:
![]()
и исключив из (16) (17) и (18) M[S] и ![]()
![]()
![]() , получаем окончательный
результат:
, получаем окончательный
результат:
![]()
Следовательно, модель, предложенная авторами, дает величину рассеивания точек попадания, пропорциональную длине пути A, а не отношению А/Т, как ошибочно полагают авторы.
2) Для подтверждения теоретических выводов авторами проделаны две серии опытов с одноприцельными движениями. В первой серии целью служил прямолинейный
130
отрезок и время движения T изменялось в пределах 200—500 мс, во второй серии прицеливание выполнялось по точке и время имело значения: 140, 170 и 200 мс. Для опытных данных нами построены аппроксимирующие формулы, удовлетворительно согласующиеся с экспериментальными точками. Для первых опытов:
![]()
для вторых опытов:
![]()
В обеих формулах We и A измеряются в см, а T — в мс.
Из рассмотрения (20) и (21) следуют два важных вывода: во-первых, не может быть сомнений в том, что рассеивание зависит от времени T, т. е. не подчиняется формуле (19), и, во-вторых, характер этой зависимости изменяется при переходе от умеренно-быстрых движений к очень быстрым.
Следовательно, модель непригодна для описания прицельного движения. Для фактически существующей зависимости рассеивания от времени движения необходимо искать другое объяснение.
3) Выполняя одиночное неприцельное движение, испытуемый должен обеспечить, чтобы по истечении заданного времени TЗ от начала движения рука оказалась на заданном расстоянии A от точки старта. Общий путь руки до остановки никакого значения не имеет. Опыты, выполненные авторами, обнаружили, что в результате тренировки общий путь значительно превышает расстояние A и рабочим участком программы движения F(t) служит начальная почти прямолинейная часть кривой (см. рис.).
Вследствие рассеивания путь S, пройденный к моменту TЗ, является случайной величиной. Найдем среднее квадратическое отклонение σ [S] при допущении: F(t) = kt (0<t< TЗ). Из сохранения формы кривой F(t) следует, что угловой коэффициент k (k = tgφ) равен:
![]()
где χ — коэффициент пропорциональности.
Скорость движения руки:
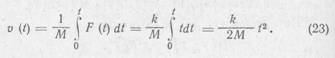
Путь, пройденный к моменту t:
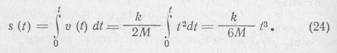
Так как s(Ta)=S, то:
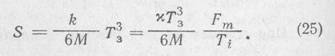
Полагая, как и выше, что σ[Ti] величина малая, линеаризуя отрезок гиперболы: 1/ Ti и используя (2), находим:
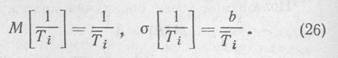
При помощи (13) находим после упрощений:
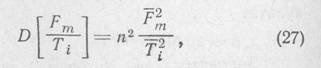
где n2=a2b2+b2+a2.
Откуда:
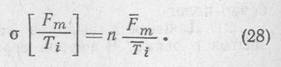
131
Используя (25) и (28), получим:
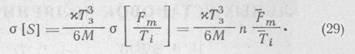
Так как
![]()
то окончательно:
![]()
Таким образом, модель, предложенная авторами, дает для одиночных неприцельных движений результат, качественно совпадающий с результатом (19) для одноприцельных движений: рассеивание пути пропорционально заданному пути и не зависит от времени. Только для неприцельных движений такой вывод согласуется с опытными данными, а для прицельных им противоречит.
4) При возвратно-поступательных неприцельных движениях рука переносится справа налево и обратно в такт с ударами метронома. Величина пути задается ориентировочно в виде двух полос, внутрь которых должны попадать точки изменения направления движения. Формально каждое отдельное движение не отличается от одноприцельного, так как и в одном и другом движении задаются путь и время. Следовательно, для возвратно-поступательных неприцельных движений справедлива формула (19). Опыты авторов показали, что рассеивание в этом случае, действительно, не зависит от времени и в первом приближении пропорционально пути. Это свидетельствует о пригодности модели для описания возвратно-поступательных неприцельных движений.
Отмеченный выше ошибочный вывод авторов о том,
что рассеивание пропорционально отношению ![]() , вынудил их
при анализе движений рассматриваемого вида для согласования теории с опытными
данными изменить одно из основных допущений модели. Вместо соотношения (1) ими
принято допущение, что рассеивание силы пропорционально
, вынудил их
при анализе движений рассматриваемого вида для согласования теории с опытными
данными изменить одно из основных допущений модели. Вместо соотношения (1) ими
принято допущение, что рассеивание силы пропорционально ![]() . Нетрудно
видеть, что это отношение пропорционально произведению FmTi.В то
время как допущение (1) имеет логическое и экспериментальное обоснования,
последнее допущение совершенно произвольно. Таким образом, одна ошибка повлекла
за собой другую.
. Нетрудно
видеть, что это отношение пропорционально произведению FmTi.В то
время как допущение (1) имеет логическое и экспериментальное обоснования,
последнее допущение совершенно произвольно. Таким образом, одна ошибка повлекла
за собой другую.
Главный итог исследования Р. Шмидта с соавторами, в отличие от выводов, сделанных самими авторами, сводится к тому, что быстрые движения в условиях, когда заданы путь и время, распадаются на два класса: прицельные и неприцельные. Точность прицельных движений растет с увеличением времени. Точность неприцельных от времени не зависит. Имеется глубокое различие в характере процесса управления этими движениями. Неприцельные движения согласуются с теорией программного управления по разомкнутой схеме. Точность прицельных движений такой теорией объяснить нельзя. Это, разумеется, не означает, что прицельное движение не содержит программно-управляемых составных частей.
1. Вентцель Е. С. Теория вероятностей. — М., 1962.
2. Schmidt R. A. A schema theory of discrete motor skill learning. Psychological Review, 1975, 82, 225—260.
3. Schmidt R. A., Zelaznik H., Hawkins В., Frank S. P., Quinn J. T. Jr. Motor-output variability: A theory for the accuracy of rapid motor acts. Psychological Review, 1979, 86 (5), 415—451.